昨天我們介紹了 McEliece Framework ，並用 RS 編碼作為例子進行實作。McEliece Framework 可以用任何編碼系統來進行實作，構造上並無限制，話雖如此，當我們在進行密碼學的安全性分析時，Hamming code 與 RS code 其實都不適合拿來實作該系統。（他們只能用於教學解說以及傳遞觀念）

Reed-Solomon碼的問題

Reed-Solomon碼具有明顯的代數結構，其生成矩陣中的代數特徵使得攻擊者可以利用這些結構來破解密碼系統。例如，Sidelnikov和Shestakov在1992年提出了一種針對基於Reed-Solomon碼的McEliece系統的攻擊方法，利用Reed-Solomon碼的代數結構來有效恢復私鑰。因此，Reed-Solomon碼在McEliece系統中的安全性不足，難以抵抗已知（非量子的）攻擊。

McEliece 本人在提出 McEliece 系統時，就使用了一種叫做 Goppa 的編碼系統，極其複雜，這讓 McEliece 系統有了足夠的安全性，已經經歷了約五十年仍未有人破解。

簡介 Goppa 碼

Goppa碼是一種特殊的代數碼，用於構建安全的糾錯碼。給定一個多項式，

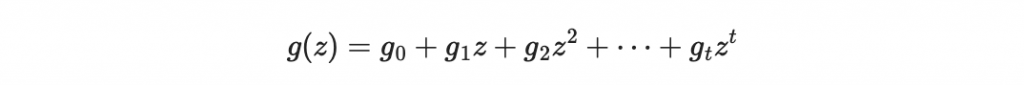
以及一個集合，

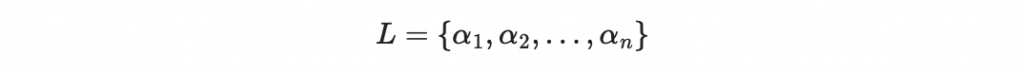
滿足

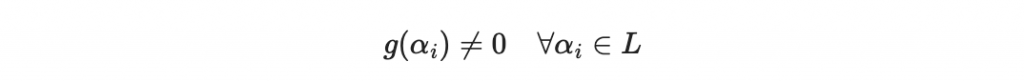
現在考慮以下集合

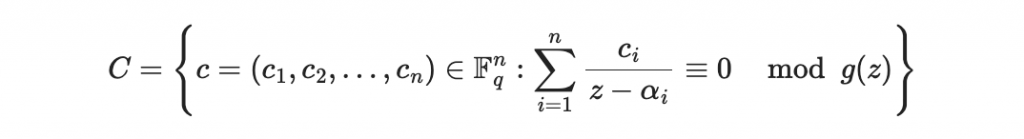
其中，

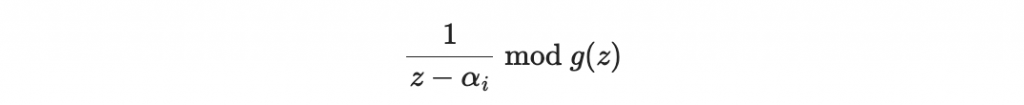
是指 (z - alpha_i) 在模除 g(z) 的多項式商環下取的乘法反元素。

如此一來 C 就成了一個向量空間，因為 c_i 要滿足特定的線性方程式，C 就正是這組線性方程式的零空間。對這個空間取基底後（任意基底）就可以形成該編碼 C 的生成矩陣 G 。

（是不是很複雜，沒關係我們就到這裡而已）

Goppa碼的特點

• 複雜的結構：（你應該已經體會到了）Goppa碼具有比Reed-Solomon碼更為隱蔽和複雜的代數結構，這使得攻擊者難以通過公鑰推斷出私鑰。

• 更正演算法：Goppa 碼跟 Hamming 碼以及 RS 碼一樣，都有已知的快速更正演算法，所以可以用在 McEliece Framework 。

一言以蔽之，RS 編碼雖然經過 S 與 P 的混淆，攻擊者不容易直接使用 RS 解碼演算法破解，但仍然有厲害的數學家做出另類的演算法來破解 RS 編碼。Goppa 編碼就數足夠複雜以致於攻擊者不好破解，但又有 Goppa 解碼演算法來讓 Alice 解出訊息。

編碼密碼學小結

在過去的幾天中，我們探索了編碼密碼學的基礎，並深入了解了幾種重要的碼及其應用，最主要就是 Hamming碼 以及 Reed-Solomon 碼。我們也介紹了McEliece密碼系統，一個基於線性碼的加密方案，其目的是利用編碼理論中的糾錯能力來「對外人隱藏訊息」。

1. 編碼理論與密碼學的結合

• 糾錯能力應用於加密：編碼理論最初是為了解決數據傳輸過程中的雜訊問題，但在密碼學中，我們故意讓 Bob （訊息傳送者）在要傳遞的碼字上加入錯誤，然後因為這個編碼有更正能力，所以 Alice 可以解回原本 Bob 傳遞的碼字。

• 不同碼的比較：在編碼密碼學中，選擇合適的碼至關重要。Hamming 能更正的錯誤不多；Reed-Solomon碼雖然具有強大的糾錯能力，但其代數結構使其易受攻擊。最後， Goppa碼因其複雜性和隱蔽性，成為最安全的選擇之一。

2. 編碼密碼學的優勢與挑戰

• 優勢：編碼密碼學的優勢在於其高效的加密和解密過程，特別是在基於Goppa碼的McEliece密碼系統中，密鑰生成和消息加密均具有較高的性能。此外，Goppa碼的安全性使其成為抗量子攻擊的理想方案。

• 挑戰：編碼密碼學的主要挑戰在於密鑰的大小。McEliece密碼系統的公鑰非常龐大，這對存儲和傳輸提出了挑戰。已經有許多研究正在想辦法減小密鑰的尺寸，但是這常常讓導致系統變得不安全。

ref:
Singh, Harshdeep. "Code based cryptography: Classic mceliece."